19. September 2023 By Simon Bächle
The path from problem to solution: how to create effective optimisation models
As part of the VideKIS research project, adesso is developing a virtual power plant in collaboration with other partners. This concept involves the aggregation of a large number of decentralised renewable energy plants to create a virtual power plant, which, in terms of its total output, can compete with nuclear power stations. These small-scale installations can pool their capacities and take part in spot and control power markets, enabling them to overcome the barriers that had prevented them from entering those markets. In this case, the aim is to offer primary control power (with the many challenges this entails) by combining small-scale plants and micro-installations. Primary control power is a form of balancing power that is brought online within a fraction of a second to offset current imbalances in the electricity grid, for example, due to a power plant outage. It helps to maintain the frequency of the power grid at a stable level of 50 Hz.
A core element of the virtual power plant is the decision on sale of electricity generated by the plants. The goal of every power plant – virtual or physical – is to achieve maximum revenue. Due most of all to the large number of markets, a decision has to be made on when to place which power plant on which market. It takes a lot of time for many power plant operators to make this decision, which is why they hire a service provider – a virtual power plant, for example – to manage their plant. The decision on when and where to sell their power must be made with care, since trading on the energy markets is associated with high profits as well as risks. Decisions typically are based on mathematical models that draw on historical data, price and weather forecasts as well as AI algorithms.
In the VideKIS project, the virtual power plant is faced with the challenge of having to decide when and where to sell the power, which is solved with the aid of an optimisation model. The aim here is to make the right decision regarding for the placement of the power plants on the market based on the results produced by the model, thus eliminating the need for humans to make these decisions.
What is an optimisation model?
An optimisation problem is a mathematical concept comparable to a complex task where you want to choose the option that delivers the best results from among several available options. This task often involves identifying the right values for specific factors (variables) in order to achieve a certain goal. As you can well imagine, this entails solving a puzzle of sorts where you have to select the right pieces to complete a picture. In this case, this would be the desired outcome. For most applications, we recommend that you start by first outlining the problem in natural language and only convert it into mathematical formulas once this step is complete.
What is the best way to create an optimisation model?
Based on the past experience gained in the research project, a best-practice approach for creating an optimisation model is described below. At the beginning, you need to define the system boundaries of the problem so that it is clear which factors and issues are to be considered and which ones are not. The research project looks into different types of power plants, including hydroelectric, wind and photovoltaic installations, along with battery storage systems and the day-ahead and primary control reserve markets.
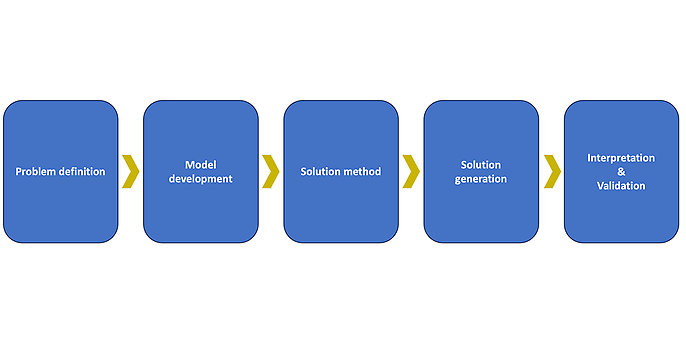
Vorgehensweise zur Erstellung eines Optimierungsmodells
Developing a model
Once the problem has been narrowed down, it is important to define a target function that quantifies the goal to be optimised. This function depends on the variables we are able to influence. These variables are usually subject to certain constraints that have to be taken into account in the model. Generally speaking, it could be either a maximisation or a minimisation problem. In most cases, power plant deployment planning seeks to maximise revenue or minimise operating costs. The goal of VideKIS is to maximise revenue, which entails the sale of electricity on the day-ahead market and the provision of primary control power.
Once the target function has been described, constraints are introduced, which are conditions or rules that limit the possible solutions. Constraints reflect real limitations or restrictions that may occur in many real-life situations. For example, they could express that power plants only have a limited capacity, that costs are associated with generating electricity or that certain regulatory requirements have to be met. It makes sense to divide the constraints into thematic blocks in order to obtain a better overview. For example, the research project defines the necessary constraints for each type of power plant.
Parameters and variables play a central role in the mathematical description of the optimisation model, since they are what enable the described problem to be defined and solved.
- Parameters are values or constants that describe the properties of an optimisation problem. They typically contain information about volumes, costs, capacities or other fixed values. These values cannot be changed, meaning they remain constant.
- Conversely, there are variables which represent the unknown values that have to be worked out in the optimisation model. They are the decisions (for example, does a power plant supplies electricity or not?) that can be made within the framework of the optimisation model in order to achieve the desired goal.
Optimisation models can be very simple or extremely complex, depending on the nature of the problem that is to be solved. This is reflected in the many different types of optimisation models that exist:
- Linear programming
- Non-linear programming
- Mixed-integer linear programming
- Dynamic programming
- Stochastic optimisation
The way in which the target function and constraints are modelled depends on the category of problem. This is also crucial to solving the problem.
Solving the optimisation model
Once the optimisation model has been described in mathematical terms by means of a target function and the desired number of constraints, it is now possible to address the question of how to solve a problem of this nature.
First off, you have to choose a suitable modelling language (GAMS, CPLEX, GUROBI and so on), which then allows you to convert the mathematical formulas into lines of code. Once the optimisation model has been described in computer code, it can then be solved using a mathematical solver. A solver is a specialised software tool that receives the developed model and searches for the best solution. As part of the process, it uses various algorithms to systematically calculate the possible solutions. This approach is largely based on the testing of various combinations of variable values. The values that maximise or minimise the target function are returned at the end of the process, whereby the constraints remain fulfilled. There are significant differences in the performance of solvers, this being mostly down to the fact that there are both commercial and non-commercial solvers available.
Interpretation and validation of the optimisation model
After one or more solutions for the optimisation model have been identified, the results must then be checked using analyses. You need to make sure that the optimal solution you identified is the right one to solve the original problem. Different test data sets should also be used to validate that the results and verify the functional principle of the model. Charts and graphs are well suited – especially when planning the deployment of power plants – for visualising the operation of the power station, for example.
Outlook
Optimisation models are in use in every industry, enabling complex problems to be solved in a short period of time. However, extensive expertise as well as mathematical and programming skills are required to create an optimisation model. If you are facing challenges like the ones described here, get in touch with us. Or visit us at the Smart Country Convention 2023, where you can speak with one of our experts.
You can find more exciting topics from the adesso world in our previous blog articles.
Also interesting:

